физика 10

_______________Урок 1 Система отсчёта

Система отсчёта состоит из: тела отсчёта, относительно которого рассматривается движение; связанной с ним системы координат; способа измерения времени.

Относительность движения задание

Интерактивный тест_1

Урок 5 Перемещение. Скорость равномерного движения.

Перемещение – вектор, соединяющий начальное и конечное положения тела. Длина траектории даёт пройденный путь s. Скорость – векторная величина, характеризующая направление и быстроту перемещения, то есть это перемещение за единицу времени. Различают мгновенную и среднюю скорости.

решим задачу Первую треть пути муравей прополз со скоростью 20 см/c, потом одну секунду простоял неподвижно, затем двигался со скоростью 30 см/с Средняя скорость пути оказалась равна 20 см/с. Найти время путешествия муравья.

решение

Мы можем мысленно разделить путь муравья на две части:
Со скоростью 20 см/с и со скоростью 30 см/с.(Которые соответственно равны 0,2 м/с и 0,3 м/с).
Рассмотрим 1/3 его пути: На это он затратил время

.
То есть 1/3S = 0,2*

Отсюда несложно выразить чему равно время:

= 10/6S
То же самое проделываем со второй его частью пути:
2/3S = 0,3*

= 20/9S
Формула средней скорости:

В нашем случае, в числитель можно поставить просто S, так как сумма расстояний и так ей равна.
В знаменателе поставим значения

и 1с:

Решая данное ур-ние, получаем S = 0,9 м
Отсюда несложно найти сумму всех времен, и она равна 4,5 с

Самостоятельно

Первую треть трассы автомобиль ехал со скоростью $60$ км/ч, вторую треть – со скоростью $120$ км/ч, а последнюю – со скоростью $110$ км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
примеры решения задач и формулы

Скоростью равномерного прямолинейного движения точки называется векторная величина, равная отношению перемещения точки к промежутку времени, в течение которого это перемещение произошло.

Интерактивный тест Вещество...

Теория_1

Теория_2

Видео урок Перемещение.

Видео перемещение при равномерном движении.

Видео Скорость

Видео_3

Примеры решения задач. Формулы

Видеоурок решение задач на графическое представление движения

Видеоурок Решение графических задач на равномерное движение

Урок 6 Уравнение прямолинейного равномерного движения

Интерактивное задание КИНЕМАТИКА

Перечень вопросов, рассматриваемых в теме: 1) основная задача механики; 2) относительность механического движения; 3) система отсчёта, материальная точка, перемещение, траектория, скорость; 4) кинематическое уравнение.

Глоссарий по теме:

Раздел механики, в котором изучается движение тел без выяснения причин, вызывающих данное движение, называют кинематикой.

Механическим движением тела называется изменение положения тела в пространстве относительно других тел с течением времени.

Материальной точкой называют тело, размерами и формой которого в условиях рассматриваемой задачи можно пренебречь. Тело, относительно которого рассматривается движение, называется телом отсчета. Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.

Траектория - линия, по которой движется точка в пространстве.

Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют путем, пройденным за этот промежуток времени.

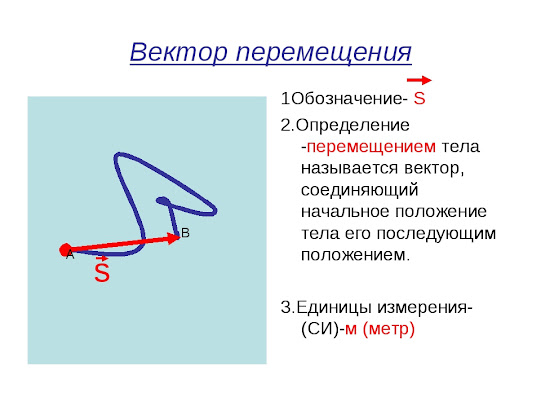
Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением.

Равномерное прямолинейное движение – это движение, при котором за любые равные промежутки времени тело совершает равные перемещения.

Скорость равномерного прямолинейного движения точки – величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло.

Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта

Теоретический материал для самостоятельного изучения

Основная задача классической механики - определить положение тела в пространстве в любой момент времени. По характеру решаемых задач классическую механику делят на кинематику, динамику и статику. В кинематике описывают движение тел без выяснения причин, вызывающих данное движение. Раздел механики, в котором изучаются причины движения, называют динамикой. Статика — раздел механики, в котором изучаются условия равновесия абсолютно твердых тел. Законы сохранения импульса и энергии являются следствиями законов Ньютонов.

Механическим движением тела называется изменение положения тела в пространстве относительно других тел с течением времени. Сформулируем закон относительности движения: характер движения тела зависит от того, относительно каких тел мы рассматриваем движение. Нет абсолютно неподвижных тел.

Рассмотрим самое простое движение – прямолинейное равномерное движение. Описать движение тела – это значит, указать способ определения его положения в пространстве в любой момент времени.

Для описания движения нужно ввести некоторые понятия: материальная точка, траектория, путь, перемещение, координата, момент времени, промежуток времени, скорость. Материальной точкой называют тело, размерами которого в условиях рассматриваемой задачи можно пренебречь. Это первая физическая модель реальных тел. Практически всякое тело можно рассматривать как материальную точку в тех случаях, когда расстояния, проходимые точками тела, очень велики по сравнению с его размерами. Например, материальными точками считают Землю и другие планеты при изучении их движения вокруг Солнца. В данном случае различия в движении разных точек любой планеты, вызванные её суточным вращением, не влияют на величины, описывающие годовое движение. Но при решении задач, связанных с суточным вращением планет (например, при определении времени восхода солнца в разных местах поверхности земного шара), считать планету материальной точкой нельзя, так как результат задачи зависит от размеров этой планеты и скорости движения точек её поверхности.

Тело, движущееся поступательно, можно принимать за материальную точку даже в том случае, если его размеры соизмеримы с проходимыми им расстояниями. Поступательным называется такое движение абсолютно твердого тела, при котором любой отрезок, соединяющий любые две точки тела, остается параллельным самому себе.

Что нужно знать для того, чтобы в любой момент времени указать положение тела? Надо, во-первых, знать, где оно было в начальный момент времени; во-вторых, каков вектор перемещения в любой момент времени. Мы уже знаем, что движение любого тела относительно. Поэтому, изучая движение тела, мы обязательно указываем, относительно какого тела это движение рассматривается. Тело, относительно которого рассматривается движение, называется телом отсчета. Чтобы рассчитать положение материальной точки относительно выбранной точки отсчета, надо связать с ним систему координат и измерить время. Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.

Рассмотрим два наиболее часто применяемых способа описания движения тел: координатный и векторный. В координатном способе положение тела в пространстве задается координатами, которые с течением времени меняются.

Рассмотрим движение материальной точки М с координатами (х, y, z) в момент времени t.

Математически это принято записывать в виде:

Количество координат зависит от условия задачи: на прямой – одна, в плоскости – две, в пространстве – три.

В векторном способе используется радиус-вектор. Радиус-вектор – это направленный отрезок, проведенный из начала координат в данную точку. Закон (или уравнение) движения в векторной форме - зависимость радиуса-вектора от времени:

Итак, для задания закона движения материальной точки необходимо указать либо вид функциональной зависимости всех трех ее координат от времени, либо зависимость от времени радиус-вектора этой точки.

Три скалярных уравнения или эквивалентное им одно векторное уравнение называются кинематическими уравнениями движения материальной точки.

Двигаясь, материальная точка занимает различные положения в пространстве относительно выбранной системы отсчета. При этом она «описывает» в пространстве какую-то линию. Линия, по которой движется точка в пространстве, называется траекторией. По форме траектории все движения делятся на прямолинейные и криволинейные. Траектория движения указывает все положения, которые занимала точка, но, зная траекторию, ничего нельзя сказать о том, быстро или медленно проходила точка отдельные участки траектории. Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют путём, пройденным за этот промежуток времени, его обозначают буквой S. Путь – скалярная величина.

Для описания движения тела нужно указать, как меняется положение точек с течением времени. Если участки криволинейные, то изменение координат тела описывают с помощью такого понятия как перемещение. Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением. Обозначается на чертежах как направленный отрезок, соединяющий начальное и конечное положение тела в пространстве:

Путь и модуль перемещения могут совпадать по значению, только в том случае, если тело движется вдоль одной прямой в одном направлении.

Важной величиной, характеризующей движение тела, является его скорость. Скорость – векторная величина. Она считается заданной, если известен ее модуль и направление. Скорость равномерного прямолинейного движения точки – векторная величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло. Пусть радиус-вектор задает положение точки в начальный момент времени t0, а радиус-вектор- в момент времени t. Тогда промежуток времени:

и перемещение:

Подставляя выражение для скорости, получим:

Если начальный момент времени t0 принять равным нулю, то скорость равна:

Выразим отсюда радиус-вектор :

Это и есть уравнение равномерного прямолинейного движения точки, записанное в векторной форме. Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий ее положение в начальный момент времени. В проекциях на ось ОХ уравнение можно записать в виде:

х=х0+vхt.

Это уравнение есть уравнение равномерного прямолинейного движения точки, записанное в координатной форме. Оно позволяет найти координату х тела при этом движении в любой момент времени, если известны проекция его скорости на ось ОX и его начальная координата х0.

Путь S, пройденный точкой при движении вдоль оси ОХ, равен модулю изменения ее координаты:

Его можно найти, зная модуль скорости

Строго говоря, равномерного прямолинейного движения не существует. Но приближенно на протяжении не слишком большого промежутка времени движение автомобиля можно считать равномерным и прямолинейным с достаточной для практических целей точностью. Таково одно из упрощений действительности, позволяющее без больших усилий описывать многие движения.

Полученные результаты можно изобразить наглядно с помощью графиков. Для прямолинейного равномерного движения график зависимости проекции скорости от времени очень прост. Это прямая, параллельная оси времени.

Как мы уже знаем, зависимость координаты тела от времени описывается формулой х=х0+𝞾хt. График движения представляет собой прямую линию:

Из второго рисунка видим, что углы наклона прямых разные. Угол наклона второй прямой больше угол наклона первой прямой , т.е за одно и тоже время тело, движущееся со скоростью , проходит большее расстояние, чем при движении со скоростью А значит А что же в случае 3, когда угол α < 0? В случае 3 тело движется в сторону, противоположную оси ОХ. Проекция скорости в случае 3 имеет отрицательное значение и график проходит ниже оси ОХ. Проекция скорости определяет угол наклона прямой х(t) к оси t и численно равна тангенсу угла

Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта. В рамках классической механики время есть величина абсолютная, то есть протекающее во всех системах отсчета одинаково.

Примеры и разбор решения заданий

1. Тело движется равномерно и прямолинейно в положительном направлении оси ОХ. Координата тела в начальный момент времени равна xо = -10м. Найдите координату тела через 5с, если модуль её скорости равен ʋ=2 м/с. Какой путь проделало тело за это время?

Дано: xо = - 10 м, t = 5 c, ʋ = 2 м/с. Найти s, х.

Решение: координату точки найдем по формуле:

х = х0 + 𝞾х t

Так как направление вектора скорости совпадает с направлением оси координат, проекция вектора скорости положительна и равна ʋx=ʋ; тогда вычисляем:

х = - 10 + 2· 5 = 0 (м).

Пройденный путь найдем s = ʋ t; s = 2·5 = 10 м.

2. Равномерно друг за другом движутся два поезда. Скорость первого равна 72 км/ч, а скорость второго — 54 км/ч. Определите скорость первого поезда относительно второго.

Дано:

Найти .

Решение: Из условия задачи ясно, что векторы скоростей поездов направлены в одну сторону. По закону сложения скоростей запишем:

где - искомая величина.

Находим проекцию скоростей на ось ОХ и записываем, чему равен модуль искомой величины

Ответ:

Формулы и задачи

Видеоурок_1

Видеоурок_2

Урок 8 Мгновенная скорость

Скорость

Скорость векторная величина, характеризующая направление и быстроту перемещения материальной точки:

В проекции на ось :

В СИ единица измерения скорости метр/секунду: $м$ .

На практике зачастую используются внесистемные единицы измерения скорости. Например, $к м ч$ .

Следует знать, что в $м с$ содержится $к м ч$ .

Скорость может изменяться во времени.

Мгновенная скорость скорость в данный момент времени в данной точке траектории. В любой точке криволинейной траектории она направлена по касательной к траектории в этой точке.

Обычно под скоростью понимают именно мгновенную скорость, т. е. скорость в определенный момент времени.

Скорость векторная величина, характеризующая направление и быстроту изменения положения тела:

В СИ единица измерения скорости метр/секунду: $м$ .

На практике зачастую используются внесистемные единицы измерения скорости. Например, $к м ч$ .

Следует знать, что в $м с$ содержится $к м ч$ .

Видеоурок_1 Мгновенная скорость.Сложение скоростей.

Видеоурок " Сложение скоростей"

Примеры решения задач_

Решение задач простых

Образец решения задачи

Моторная лодка, плывя, держит курс перпендикулярно к течению реки, имея скорость 32,3 км/ч, переплывает реку шириной 0,3 км. Скорость течения реки — 9 км/ч. Найди перемещение моторной лодки от начала движения.

Ответ (ответ и промежуточные вычисление округли до сотых): км.

_______________________________

Запишем краткое условие к этой задаче.

Дано:

∣∣∣V→1∣∣∣=32,3 км/ч;

∣∣∣V→2∣∣∣=9 км/ч;

|S|=0,3 км;

|r|−?

Обозначим скорость моторной лодки

V→1, а скорость течения реки

V→2.

Покажем на рисунке, как направлены векторы их скоростей.

Естественно, моторная лодка не сможет уже плыть прямо. Течение реки будет действовать вправо и моторная лодка начнёт смещаться понемногу в ту сторону, куда оно направлено.

Покажем, как точно будет направлен результирующий вектор скорости.

Для этого нужно сложить скорости

V→1 и

V→2 по правилу треугольника или по правилу параллелограмма.

Правильно это сделать так:

Выстраиваем их друг за другом, чтобы получились стороны треугольника.

Или соединяем начала этих векторов — тогда используем правило параллелограмма.

Для сложения по правилу треугольника просто соединяем начало первого вектора с концом последнего.

Для сложения по правилу параллелограмма дорисовываем ещё две стороны напротив уже имеющихся двух.

Должен получиться один и тот же вектор

V→. Нарисуем его красным цветом.

Моторная лодка плывёт, но сносится течением реки.

Найдём, с какой скоростью

V→ происходит движение моторной лодки.

Как видно, у нас получился прямоугольный треугольник с катетами

V→1 и

V→2, а также гипотенузой

V→.

Найдём гипотенузу

V→ по теореме Пифагора:

∣∣∣V→∣∣∣=(∣∣∣V→1∣∣∣)2+(∣∣∣V→2∣∣∣)2−−−−−−−−−−−−−−−−−√.

Численно получим:

∣∣∣V→∣∣∣=(32,3)2+(9)2−−−−−−−−−−−√=33,53 км/ч.

Как видно, со скоростью 33,53 км/ч моторная лодка преодолеет расстояние АВ. Именно оно и равно нашему перемещению

r от начала движения. Чтобы его найти, необходимо сначала найти время

t, требующееся моторной лодке , чтобы переплыть реку. Для этого необходимо всё расстояние

|S|=0,3 км разделить на скорость моторной лодки

V→1, т. к. именно с этой скоростью моторная лодка стремится к берегу.

t=SV→1=0,332,3=0,01 ч.

Теперь, когда у нас есть значение времени

t и скорости

V→, можем найти перемещение

r моторной лодки от начала движения, перемножив их.

Получим:

r=V→⋅t=33,53⋅0,01=0,34 км.

Итак, перемещение моторной лодки от начала движения составило 0,34 км.

Пример решения задачи на движение под прямым углом

Резиновая лодка,плывя,держит курс под углом 90 градусов к течению реки

развивая скорость 33,6 км/ч, переплывает реку шириной 1,1 км. Значение скорости течения реки — 9 км/ч. Определи перемещение резиновой лодки от начала движения.

Ответ (ответ и промежуточные вычисление округли до сотых):

Решение

Согласно рисунку найдем результирующий вектор скорости по теореме Пифагора

Vr=√Vp^2 + Vp^2=√2.2^2+4.9^2=5.37м/с

Результирующий вектор скорости совпадает с вектором перемещения лодки под действием течения реки.

Углы при векторах скоростей катера и результирующей скорости катера совпадает с углом перемещения лодки .

треугольники скоростей и перемещений подобны.

тогда Sp/Vл=Sл/Vr

365/4,9=Sл/5,37

Sл=365*5,37/4,9=400м

перемещение надувной лодки от начала движения = 400м

Урок 8 Ускорение. Скорость при движении с постоянным ускорением.

Уравнение равноускоренного движения.

Ускорением тела при равноускоренном движении называют векторную физическую величину, равную отношению изменения скорости тела к промежутку времени, за который это изменение произошло.

menu_new

физика 10

Скорость

развивая скорость 33,6 км/ч, переплывает реку шириной 1,1 км. Значение скорости течения реки — 9 км/ч. Определи перемещение резиновой лодки от начала движения.

Решение задач. Равноускоренное движение (достаточный уровень)

Комментариев нет:

Отправить комментарий

счётчик

Форма обратной связи